数据的表示和运算

1、数字与编码

1.1 进位计数制及相互转换

• 二进制
• 八进制
• 十进制
• 十六进制

1.1.1 二进制、八进制和十六进制转十进制

任意进制转十进制：数码与权值相乘，再把乘积相加

1.1.2 二进制转八进制和十六进制

二进制转八/十六进制

小数点前：右起往左数，三位/四位一组

小数点后：左起往右数，三位/四位一组

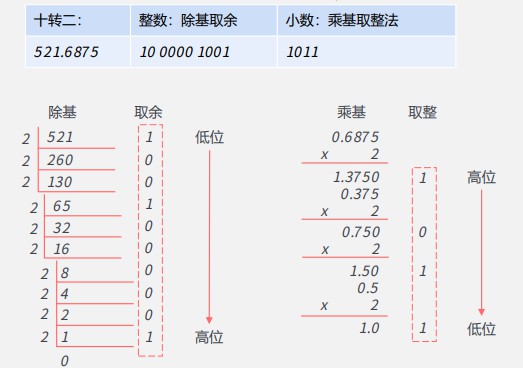
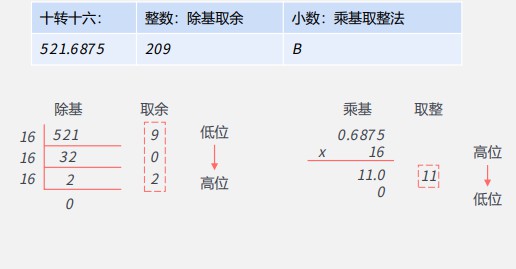
1.1.3 十进制转其他进制

整数部分：除基取余法

小数部分：乘基取整法

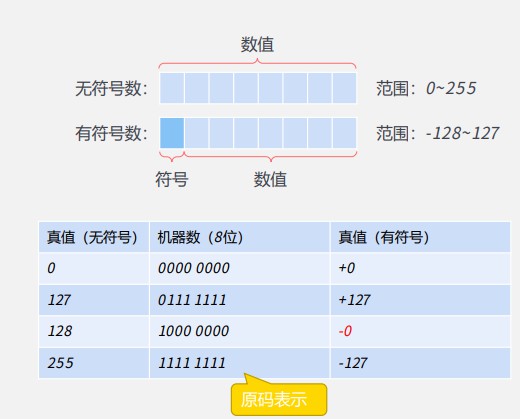
1.2 真值和机器数

**真值：**符号（+-） + 绝对值

**机器数：**符号和数值一起编码

• 无符号数： 每个bit位都是数值位 只有正数和0
• 有符号数： 最高位代表符号：0正，1负 正负数各占一半（含0）

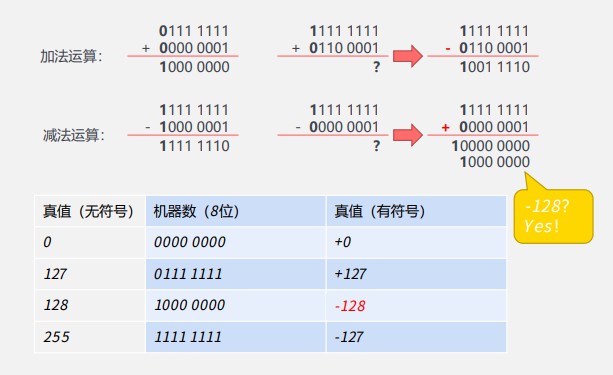
1.2.1 源码的加减运算

原码的加法运算：

• 同号加，异号减
• 取大绝对值符号

原码的减法运算：

• 同号减，异号加
• 大绝对值 - 小绝对值
• 取大绝对值符号

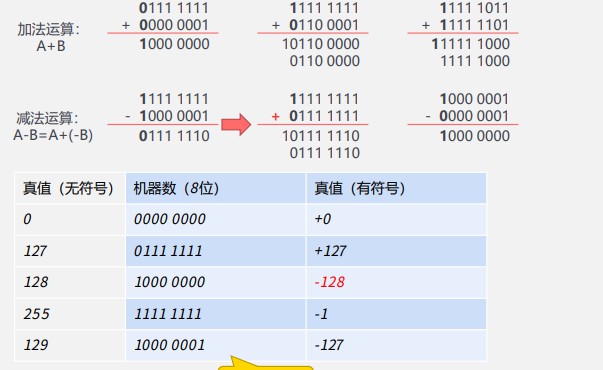
1.2.2 补码的加减运算

正数的原码、反码、补码都一样

原码：符号位 + 数值位

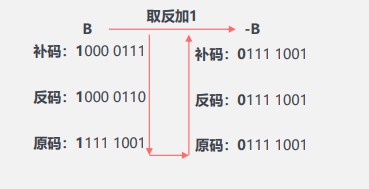
-反码：符号位不变，数值位取反

补码：反码 + 1

计算机中数的存储和运算，都使用补码

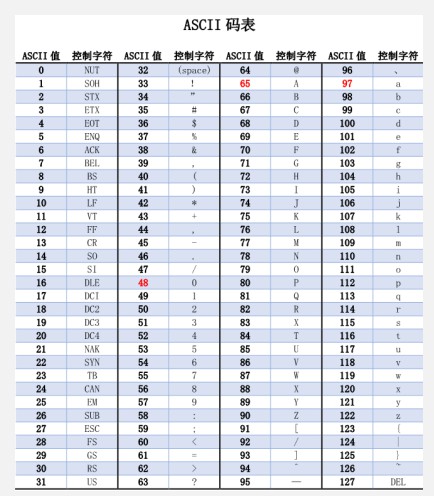
1.3 字符和汉字编码

• ASCII：美国标准信息交换码 共128个字符

  

• 汉字编码

  GBK2312，GB18030，GBK 一个汉字占两个字节

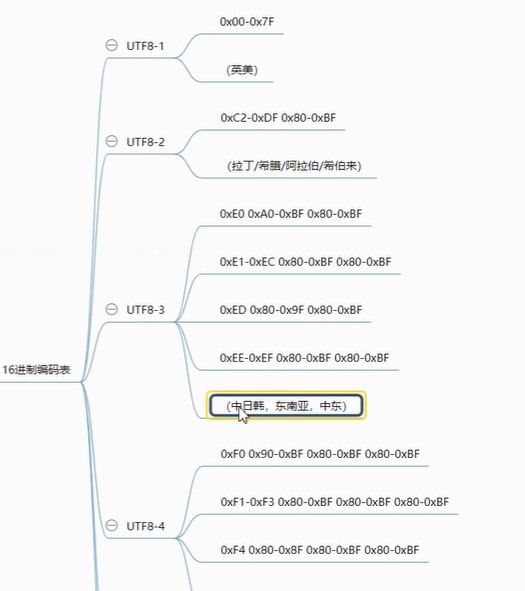
  UTF-8/UTF8：

  国际通用字符集，兼容ASCII码 使用1-4个可变长度字节编码

2、数的表示和运算

2.1 定点数的表示和运算

2.1.1 定点数的表示

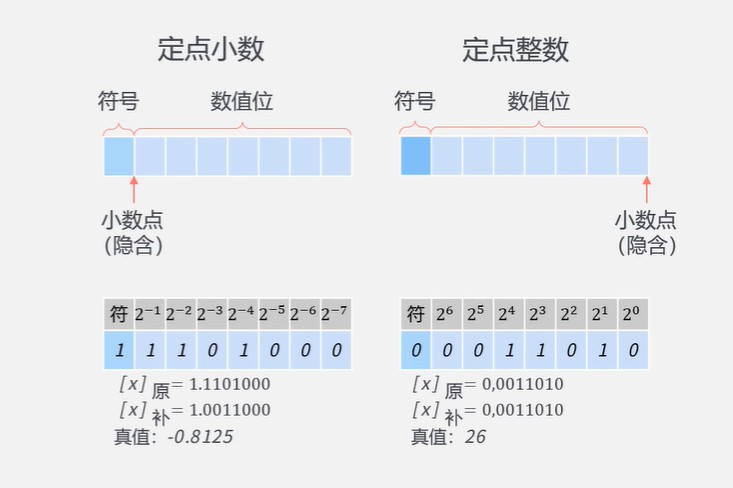
**定点数：**小数点位置是固定的，但不需要点号

**定点小数：**即纯小数 小数点在符号位之后，有效数值位之前 范围（补码）： −1 ≤ 𝑥 ≤ 1 − 2 ^N

**定点整数：**即纯整数 小数点在有效数值位之后 范围（补码）：−2 ^N ≤ 𝑥 ≤ 2 ^N − 1

**优点：**定点运算简单，实现容易

**缺点：**表示范围小，运算精度低，不适合科学运算

2.1.2 定点数的加减运算

定点整数的运算：

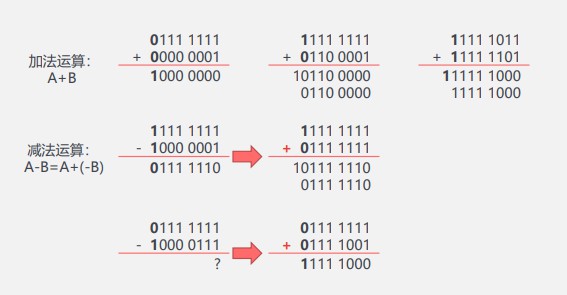
**算数运算：**加减乘除（补码）， 把减法转成加法：A-B=A+(-B)

2.1.3 定点数的乘除运算

定点整数的运算：

**算数运算：**加减乘除（补码） 把乘法转成累加 把除法转成累减 减->加

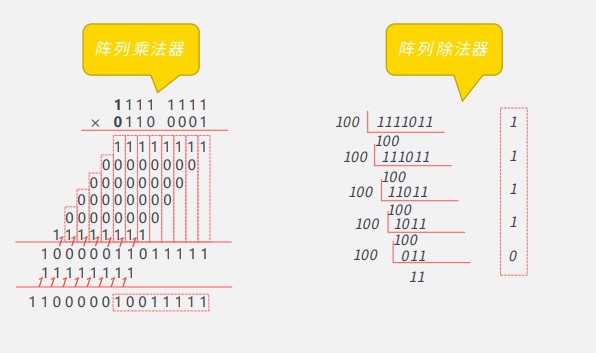
2.1.4 逻辑&按位运算

一个数和另外一个数异或两次等于这个数本省身

算数运算：+、-、×、/

**逻辑运算：**与&、或| 、非!

按位运算：&、|、^、~

• 按位与&：同1则1，不同则0
• 按位或|：有1则1
• 按位异或^：同0，异1
• 按位取反~：0变1，1变0

按位运算：&、|、^、~、<<、>>、>>>

• 左移<<：向左平移，右边补0
• 右移>>：向右平移，左边补符号位
• 无符号右移>>>：向右平移，左边补0

2.2 浮点数的表示和运算

2.2.1 浮点数的表示

小数点位置是不固定的，根据需要浮动 任何一个R进制数N，可以表示为：

(𝑁)𝑅= ±𝑆 × 𝑅 ^±e

S-尾数：N的有效数字，反映了数的精度

常用补码表示的定点小数 尽可能占满尾数，保留更多有效数字

R-基值：即进制数，2/4/8/16等

e-阶码：小数点的实际位置，反映了表示范围 常用补码表示的定点整数

数符；阶符

2.2.2 浮点数的规格化

**规格化：**尾数的最高数值位必须有效（非0） 左规：最高数值位无效，尾数左移，阶码减1 右规：尾数“假溢出”，右移，阶码加1

2.2.3 浮点数的加减运算

步骤

• 对阶：使阶码相等（小->大）
• 尾数求和/差
• 规格化
• 舍入：
  • 截断法（恒舍法）：强制舍去
  • 0舍1入法：舍弃位的最高位为1，则进1
  • 恒置1法：末位恒置1
• 判断溢出：
  • 阶码上溢（异常）；阶码下溢（作0）

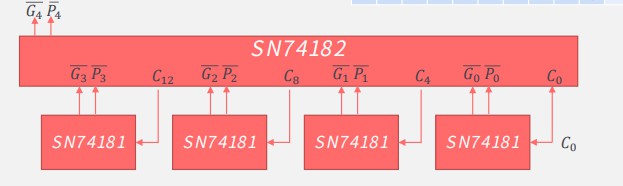
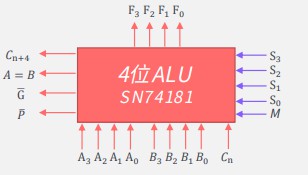
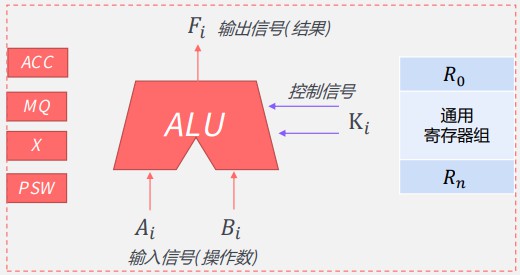
3、算数逻辑单元ALU

3.1 ALU的功能和结构

算数运算：加/减/乘/除

逻辑运算：与/或/非

辅助功能：移位/求补

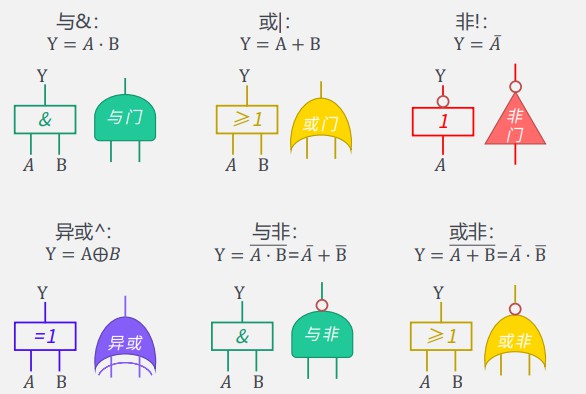
3.1.1 基本逻辑运算的实现

与&：Y = 𝐴 · B

或|： Y = A + B

非!： Y = 𝐴ҧ

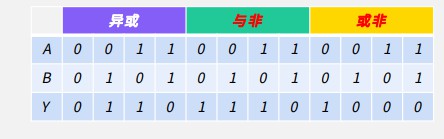
异或^: Y = A⨁𝐵

与非： Y = 𝐴 · B=𝐴ҧ+ Bഥ

或非： Y = 𝐴 + B=𝐴ҧ· B

3.2 串行加法器和并行加法器

3.2.1 一位全加器

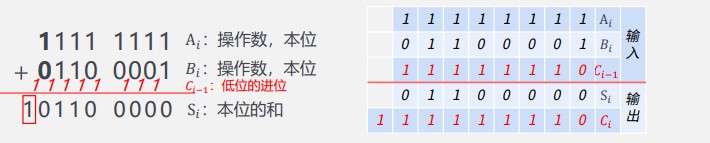
逻辑电路

3.2.2 串行加法器

进位触发器：保存 进位 位

数据逐位送入FA中运算

串行、逐位送回寄存器

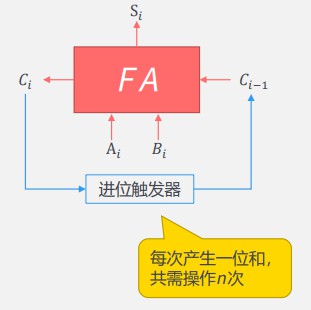
逻辑电路

3.2.3 并行加法器

把n个全加器串接起来

串行进位：进位信号逐级形成

运算速度取决于每一个进位的产生速度

改进：A𝑛~𝐴0，𝐵𝑛~𝐵0是已知的