算法结构体系

第1节： 复杂度、对数器、二分法

1.1 复杂度

1.1.1 常数操作

了解复杂度之前需要了解一下常数操作，所谓常数操作也可以称之为固定时间的操作

比如说：两个int类型的数相加、相减少等，同时无论数值大小，1加1也好，1111111加2222222也好，做种都是32位二进制相加，虽然相加数值相差很大，但实际上计算时间基本相同。

再比如说数组的寻址：获取数组第100万个数据，和200万个数据时间基本相同，因为数组在内存中是连续的，获取数据只需要计算其偏移量即可

但是链表比如linkedlist，获取第100万个数据，和200万个数据时间就不是固定的。

1.1.2 时间复杂度

常数时间的操作：如果一个操作的执行时间不以具体样本量为转移，每次执行时间都是固定时间。称这样的操作为常数时间的操作。

常见的常数时间的操作：

• 常见的算术运算（+、-、*、/、% 等）
• 常见的位运算（>>、>>>、<<、|、&、^等）
• 赋值、比较、自增、自减操作等
• 数组寻址操作

确定算法流程的总操作数量与样本数量之间的表达式关系

只看表达式最高阶项的部分

1.1.3 空间复杂度

出本身外算法需要额外创建的空间

1.1.4 常数项

当两个算法的相同时间复杂度，就需要比较常数项，不如插入排序比冒泡排序好。、

1.1.5 算法最优解

• 时间复杂度最低
• 空间复杂度尽量少

1.1.6 排名从好到差

O(1)
O(logN)
O(N)
O(N*logN)
O(N^2) O(N^3) … O(N^K) O(2^N) O(3^N) … O(K^N) O(N!)

1.2 选择、冒泡、插入排序

1.2.1 选择排序

外层循环：控制循环次数，也可以叫几个轮回

内层循环：获取最小数或者最大数，放在第一个数

public static void main(String[] args) {
    int[] arr = {3,5,2,9,6,7};

    // 3,5,2,9,6,7
    // 2,3,5,9,6,7 内存第一次循环结束
    // 2,3,5,9,6,7 内存第二次循环结束
    //.......

    selectSort(arr);
    System.out.println(Arrays.toString(arr));
}

/**
     * 选择排序
     * @param arr
     */
private static void selectSort(int[] arr) {
    if(arr == null || arr.length < 2) return;

    for (int i = 0; i < arr.length - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            // 这里也可以不用记录需要交换的索引，直接交换值(考虑到可能平凡交换这里就记录后面最大值的索引)
            if(arr[minIndex] > arr[j]) minIndex = j;
        }
        // 不相等，说明存在更小的值
        if(i != minIndex) swap(arr, i, minIndex);
    }
}

/**
     * 交换
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

1.2.2 冒泡排序

两两比较，如果左边大于右边，交换，实现从小到大排序

public static void main(String[] args) {
    int[] arr = {3,5,2,9,6,7};

    // 3,5,2,9,6,7
    // 3,2,5,6,7,9 内存第一次循环结束
    // 2,3,5,6,7,9 内存第二次循环结束
    //.......

    bubbleSort(arr);
    System.out.println(Arrays.toString(arr));
}

/**
     * 冒泡排序排序
     * @param arr
     */
private static void bubbleSort(int[] arr) {
    if(arr == null || arr.length < 2) return;

    // 外层控制循环次数
    for(int i = 1 ; i < arr.length ; i++) {
        // 内层相邻值比较
        for (int j = 0; j < arr.length - i; j++) {
            if(arr[j] > arr[j + 1]) swap(arr, j, j + 1);
        }
    }
}

/**
     * 交换
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

1.2.3 插入排序

类似于摸牌，每摸一张然后从右往左比较插入合适位置

public static void main(String[] args) {
    int[] arr = {3,5,2,9,6,7};

    // 3,5,2,9,6,7
    
    // 3,5
    // 3,5,2       => 2,3,5
    /// 2,3,5,9    => 2,3,5,9
    // ...

    insertSort(arr);
    System.out.println(Arrays.toString(arr));
}

/**
     * 插入排序
     * @param arr
     */
private static void insertSort(int[] arr) {
    if(arr == null || arr.length < 2) return;

    // 3,5
    // 3,5,2 => 2,3,5

    for (int i = 1; i < arr.length; i++) {
        for (int j = i; (j - 1) >= 0; j--) {
            if(arr[j] < arr[j - 1]) swap(arr,j , j - 1);
        }
    }

}

/**
     * 交换
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

1.2 对数器

1，你想要测的方法a 2，实现复杂度不好但是容易实现的方法b 3，实现一个随机样本产生器 4，把方法a和方法b跑相同的随机样本，看看得到的结果是否一样 5，如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a和方法b 6，当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

数组随机数

/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }

    return arr;
}

1.3 二分法

1, 在一个有序数组中，找某个数是否存在

2, 在一个有序数组中，找>=某个数最左侧的位置

3, 在一个有序数组中，找<=某个数最右侧的位置

4, 局部最小值问题

二分查找

public static void main(String[] args) {
    // 数组长度
    int len = 10;
    // 元素最大值
    int maxVal = 50;
    // 生成随机数组
    int[] arr = generateRandomArray(len, maxVal);

    // 排序
    Arrays.sort(arr);
    System.out.println(Arrays.toString(arr));



    // 二分查找
    int targetVal = arr[3];
    int taggetIndex = halfSearch(arr, targetVal);
    System.out.println("taggetIndex：" + taggetIndex);
}

/**
     * 二分查找
     * @param arr
     * @param targetVal
     * @return
     */
private static int halfSearch(int[] arr, int targetVal) {
    int left = 0;
    int right = arr.length - 1;
    int mid = 0;
    while (left <= right) {
        // (left + rignt) / 2 当left和right数据很大时，相加存在越界的情况
        mid = left + ((right - left) >> 1);
        if(arr[mid] < targetVal)
            left = mid + 1;
        else if(arr[mid] > targetVal)
            right = mid - 1;
        else
            break;
    }
    return mid;
}

/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

局部最小

• 无序数组，并且相邻数不相等，只需要找出一处即可
• 0位置数小于1位置数，0为局部最小
• N位置数小于N-1位置数，N为局部最小

思路：

• 可以使用二分查找

• 先抠边界判断

• 如果两个边界不存在局部最小，画个图，说明中间存在局部最小

第2节：异或运算相关面试题

2.1 异或

**异或定义：**相同为零，不同为1 (也称为无进位相加)

异或特性：

• 0异或任何数等于其本身
• 任何数异或自生结果为0
• 一个数异或一个数两次，结果为这个数本身
• 异或的数满足交换律和结合律

两数交换，不需要采用额外空间

int a = 1;
int b = 2;

a = a ^ b;
b = a ^ b;
a = a ^ b;

**注意：**相同数或者相同位置的数不能使用，相同数异或为0

2.1.1 题目

一个数组中，只有一种数出现奇数次，其余的都是出现偶数次，找出这个出现奇数次的数

**思路：**相同的数异或为0，一个数异或0等于其自身

怎么把一个int类型的数，提取出最右侧的1来

思路：

• 一个数取反加一等一这个数的相反数 -a = (~a) + 1

0000 1100

1111 0011 取反  

1111 0100 加一

&

0000 1100 &上数本身

0000 0100  这个数就是需要的结果

总结：

a & (~a + 1)  =>  a & -a

一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数

思路：

• 这些数异或，最终结果为这两个奇数相异或
• 由于这两个数不相等，异或的结果指定不为0
• 这样就可以找出最右侧唯一的数（1100 =》 0100）,说明这两个奇数在此位置是不同的
• 根据这这位是否为0，分成两组，分别异或就可以得到这两个数

public static void main(String[] args) {
    int[] arr = {3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6};

    // 得到两个奇数异或值
    int eor = 0;
    for (int element : arr) {
        eor ^= element;
    }

    // eor的值为这两个奇数的异值

    // 找出最右侧为1的值，因为最右侧为1的数，代表这两个奇数在此位上是不同的

    int bitV = eor & (~eor + 1);

    // 根据这个位上为1或者不唯一进行分类，将这两个奇数分开

    // 第一个奇数
    int oneV = 0;
    for (int element : arr) {
        // 该位置上为0的都异或上
        if((element & bitV) == 0) {
            oneV ^= element;
        }
    }
    System.out.println("第一个奇数：" + oneV);
    System.out.println("第二个奇数：" + (eor ^ oneV));
}

一个数组中有一种数出现K次，其他数都出现了M次， M > 1, K < M 找到，出现了K次的数

要求，额外空间复杂度O(1)，时间复杂度O(N)

思路：

• 空间复杂度为O(1)，因此哈希表的方式不可取

• 定义一个32位长度的数组

• 将这些数对应的位置在这数组上事项相加

  a=3  ...0011
  b=5  ...0101
  
  在数组中表示为：...0112
  
  

• 按上面计算完可以得到一个数组，然后将数据的每位数 M取模，如果为0代表出现k次的数在此位置上为0，相反为1

 public static void main(String[] args) {
      int[] arr = {13,66,55,66,13,55,66,55,55,13,66,55,66,13,55,66};

      int k = 4, m = 6;

      // 定义零时数组防止各位数之和
      int[] temp = new int[32];

        for (int ele : arr) {
            for (int i = 0; i < 32; i++) {
//                if(((ele >> i) & 1) != 0)
//                    temp[i] ++;
//                简写为： temp[i] += ((ele >> i) & 1);
                    temp[i] += ((ele >> i) & 1);
            }
        }

        System.out.println(Arrays.toString(temp));

        int res = 0;

        for (int i = 0; i < 32; i++) {
            if((temp[i] % m) != 0) {
                res |= (1 << i);
            }
        }
        System.out.println("出现k次的数为：" + res);
    }

对数器校验：

• 编写一个简单程序和上面程序对位对比
• 编写对数器

/**
     * 一个数组中有一种数出现K次，其他数都出现了M次，
     * M > 1,  K < M
     * 找到，出现了K次的数
     * 要求，额外空间复杂度O(1)，时间复杂度O(N)
     *
     * 这里采用对数器进行校验
     */
public static void main(String[] args) {
    // 测试次数
    int testTime = 100;
    int kMMax = 9;
    for (int i = 0; i < testTime; i++) {
        // 生成 k,m
        int a = (int)(Math.random() * kMMax) + 1; //[1,9]
        int b = (int)(Math.random() * kMMax) + 1; //[1,9]
        int k = Math.min(a, b);
        int m = Math.max(a,b);
        if(k == m) m++;
        System.out.println("k:" + k + ",m:" +m);
        int[] arr = generateLCArr(k, m, 100, 3);
        System.out.println(Arrays.toString(arr));
        int val1 = onlyTimes(arr, k, m);
        int val2 = test(arr,k,m);
        if(val1 != val2) System.out.println("出错了~~：" + Arrays.toString(arr));
    }
}

/**
     * 测试案例
     * @param arr
     * @param k
     * @param m
     * @return
     */
private static int test(int[] arr, int k, int m) {
    HashMap<Integer, Integer> map = new HashMap<>();

    // hash映射
    for (int ele : arr) {
        map.put(ele, map.getOrDefault(ele,0) + 1);
    }

    for (Integer key : map.keySet()) {
        Integer value = map.get(key);
        if(value ==  k) {
            return key;
        }
    }
    return -1;
}

private static int onlyTimes(int[] arr, int k, int m) {
    // 定义零时数组防止各位数之和
    int[] temp = new int[32];

    for (int ele : arr) {
        for (int i = 0; i < 32; i++) {
            temp[i] += ((ele >> i) & 1);
        }
    }

    int ans = 0;

    for (int i = 0; i < 32; i++) {
        if((temp[i] % m) != 0) {
            ans |= (1 << i);
        }
    }
    return ans;
}

/**
     * 生成对对数器数组
     * @param k k次
     * @param m m次
     * @param range 范围
     * @param sampleNum 样品数
     * @return
     */
public static int[] generateLCArr(int k, int m, int range, int sampleNum) {
    // 创建返回数组
    int[] arr = new int[k + (sampleNum - 1) * m];
    int arrIndex = 0;

    HashSet<Integer> sets = new HashSet<>();
    // 生成 k数 [0, range]
    int kNum = (int) (Math.random() * range) + 1;

    // 将出现k的数添加到数组中
    for (; arrIndex < k; arrIndex++) {
        arr[arrIndex] = kNum;
    }

    // 添加集合中避免后续生成重复
    sets.add(kNum);


    sampleNum--;
    // 添加出现过m次的数
    for (int i = 0; i < sampleNum; i++) {
        // 出现m次的随机数 生成随机数
        int mVal = 0;
        do {
            mVal =  generateMVal(range);
        }while (sets.contains(mVal));
        sets.add(mVal);

        // 添加至数组中
        for (int j = 0; j < m; j++) {
            arr[arrIndex++] = mVal;
        }
    }

    return arr;
}

/**
     * 生成m值 [-range, range]
     * @param range
     * @return
     */
private static int generateMVal(int range) {
    return ((int)( Math.random() * range)  + 1) - ((int) (Math.random()  * range) + 1);
}

第3节：基础的数据结构

3.1 单项链表和双向链表

单向链表节点结构（可以实现成范型）

public class Node {
    public int value;
    public Node next;
    public Node(int data) {
        value = data;
    }
}

双向链表节点结构

public class DoubleNode {
    public int value;
    public DoubleNode last;
    public DoubleNode next;

    public DoubleNode(int data) {
        value = data;
    }
}

3.1.1 单链表反转

a -> b -> c => c -> b -> a

/**
 * 节点
 */
class Node {

    public Integer value;

    public Node next;

    public Node(Integer value) {
        this.value = value;
    }

}

/**
     * 单链表反转
     */
public static void main(String[] args) {
    Node head = new Node(1);
    head.next = new Node(2);
    head.next.next = new Node(3);
    head.next.next.next = new Node(4);

    // 处理前输出
    printList(head);

    head = reverse(head);

    // 处理后输出
    printList(head);

}

/**
     * 打印链表
     * @param head
     */
private static void printList(Node head) {
    StringBuilder sb = new StringBuilder();
    while (head != null) {
        sb.append(head.value);
        sb.append(" -> ");
        head = head.next;
    }
    sb.delete(sb.length() - 4, sb.length());
    System.out.println(sb.toString());
}

/**
     * 单链表反转
     * @param head
     * @return
     */
private static Node reverse(Node head) {
    Node pre = null;
    Node next = null;

    while (head != null) {
        next = head.next;
        head.next = pre;
        pre = head;
        head = next;
    }
    return pre;
}

3.1.2 双链表反转

/**
 * 节点
 */
class DoubleNode {

    public Integer value;

    public DoubleNode last;

    public DoubleNode next;

    public DoubleNode(Integer value) {
        this.value = value;
    }

}

/**
     * 双链表反转
     */
public static void main(String[] args) {
    DoubleNode node1 = new DoubleNode(1);
    DoubleNode node2 = new DoubleNode(2);
    DoubleNode node3 = new DoubleNode(3);
    DoubleNode node4 = new DoubleNode(4);
    node1.next = node2;
    node1.last = null;

    node2.next = node3;
    node2.last = node1;

    node3.next = node4;
    node3.last = node2;

    node4.next = null;
    node4.last = node3;

    System.out.println("初始状态");
    printNextList(node1);
    DoubleNode reverse = reverse(node1);
    // 反转后状态
    printNextList(reverse);
}

/**
     * 打印链表
     * @param head
     */
private static void printNextList(DoubleNode head) {
    StringBuilder sb = new StringBuilder();
    while (head != null) {
        sb.append(head.value);
        sb.append(" -> ");
        head = head.next;
    }
    sb.delete(sb.length() - 4, sb.length());
    System.out.println(sb.toString());
}

/**
     * 打印链表
     * @param head
     */
private static void printLastList(DoubleNode head) {
    StringBuilder sb = new StringBuilder();
    while (head != null) {
        sb.append(head.value);
        sb.append(" -> ");
        head = head.last;
    }
    sb.delete(sb.length() - 4, sb.length());
    System.out.println(sb.toString());
}

/**
     * 单链表反转
     * @param head
     * @return
     */
private static DoubleNode reverse(DoubleNode head) {
    DoubleNode pre = null;
    DoubleNode next = null;

    while (head != null) {
        next = head.next;
        head.next = pre;
        head.last = next;
        pre = head;
        head = next;
    }
    return pre;
}

3.1.3 把给定的值都删除

举例：

2 —> 3 —> 7 —> 0 —>2 —> 2

将2都删除

思路：

• 由于存在头结点就需要删除的情况，先找出从头开始第一个不需要删除的节点

• 定义另个变量，pre和cur

• cur用来判断是当前值和需要被删除的值是否一样

  • 如果不一样，pre被赋值为为当前值，cur向后一定一个节点
  • 如果一样，说明这个数是不需要的只需要将pre的next下一个值指向这个数的下一个值

/**
     * 删除指定数
     * @param args
     */
public static void main(String[] args) {
    // 链表长度
    int listLen = 10;

    // 链表最大值
    int maxNum = 10;

    // 测试次数
    int testTimes = 100;

    for (int i = 0; i < testTimes; i++) {

        Node orgHead = generateNode(listLen, maxNum);
        int deleteNum = ((int)(Math.random() * maxNum ) + 1);
        System.out.println("原始链表：");
        printList(orgHead);
        System.out.println("需要删除的数为：" + deleteNum);
        // 对数器方法
        Node head01 = test(orgHead, deleteNum);
        // 实际方法
        Node head02 = deleteNum(orgHead, deleteNum);
        boolean compare = compare(head01, head02);
        System.out.println("结果：" + compare);
        printList(head01);
        printList(head02);

    }
}

/**
     * 比较
     * @param head01
     * @param head02
     */
private static boolean compare(Node head01, Node head02) {

    List<Integer> val1s = new ArrayList();
    List<Integer> val2s = new ArrayList();

    while (head01 != null) {
        val1s.add(head01.value);
        head01 = head01.next;
    }

    while (head02 != null) {
        val2s.add(head02.value);
        head02 = head02.next;
    }

    if(val1s.size() != val2s.size()) return false;

    for (int i = 0; i < val1s.size(); i++) {
        if(val1s.get(i) != val2s.get(i)) return false;

    }
    return true;
}

/**
     * 删除数
     * @param head
     * @param deleteNum
     * @return
     */
private static Node deleteNum(Node head, int deleteNum) {
    // 由于存在头结点就需要删除的情况，先找出从头开始第一个不需要删除的节点
    while (head != null) {
        if(!head.value.equals(deleteNum)) break;
        head = head.next;
    }
    Node cur = head;
    Node pre = head;
    while (cur != null) {
        if(cur.value == deleteNum)
            pre.next = cur.next;
        else
            pre = cur;

        cur = cur.next;
    }
    return head;
}

/**
     * 对数器方法
     * @param head
     * @return
     */
private static Node test(Node head, Integer deleteNum) {
    List<Integer> vals = new ArrayList();

    while (head != null) {
        if(head.value != deleteNum)
            vals.add(head.value);
        head = head.next;
    }

    if(vals.size() == 0) return null;

    head = new Node(vals.get(0));
    Node tail = head;
    for (int i = 1; i < vals.size(); i++) {
        tail.next = new Node(vals.get(i));
        tail = tail.next;
    }
    return head;
}

/**
     * 生成链表
     * @param listLen
     * @param maxNum
     * @return
     */
private static Node generateNode(int listLen, int maxNum) {

    int headVal = (int)(Math.random() * maxNum ) + 1;
    Node head = new Node(headVal);
    Node tail = head;

    listLen--;

    for (int i = 0; i < maxNum; i++) {
        int value = (int)(Math.random() * maxNum ) + 1;
        Node node = new Node(value);
        tail.next = node;
        tail = node;
    }
    return head;

}

/**
     * 打印链表
     * @param head
     */
private static void printList(Node head) {
    StringBuilder sb = new StringBuilder();
    while (head != null) {
        sb.append(head.value);
        sb.append(" -> ");
        head = head.next;
    }
    sb.delete(sb.length() - 4, sb.length());
    System.out.println(sb.toString());
}

3.2 队列和栈

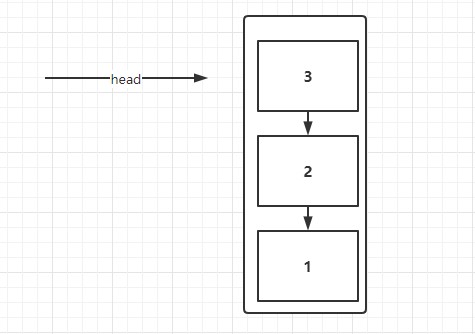
栈：数据先进后出，犹如弹匣

队列：数据先进先出，好似排队

3.2.1 双向链表实现栈

class LLForStack {

    DoubleNode head;

    public void add(Integer ele) {
        DoubleNode node = new DoubleNode(ele);
        if(head == null) {
            head = node;
        }else {

            node.next = head;
            head.last = node;
            head = node;
        }
    }

    public Integer poll() {
        if(head == null) {
            return null;
        }
        Integer ans = head.value;
        head = head.next;

        if(head != null)
            head.last = null;

        return ans;
    }
}

/**
     * 双向链表实现栈
     * @param args
     */
public static void main(String[] args) {
    LLForStack stack = new LLForStack();

    stack.add(1);
    stack.add(2);
    stack.add(3);
    stack.add(4);


    System.out.println(stack.poll());
    System.out.println(stack.poll());
    System.out.println(stack.poll());
    System.out.println(stack.poll());
    System.out.println(stack.poll());

}

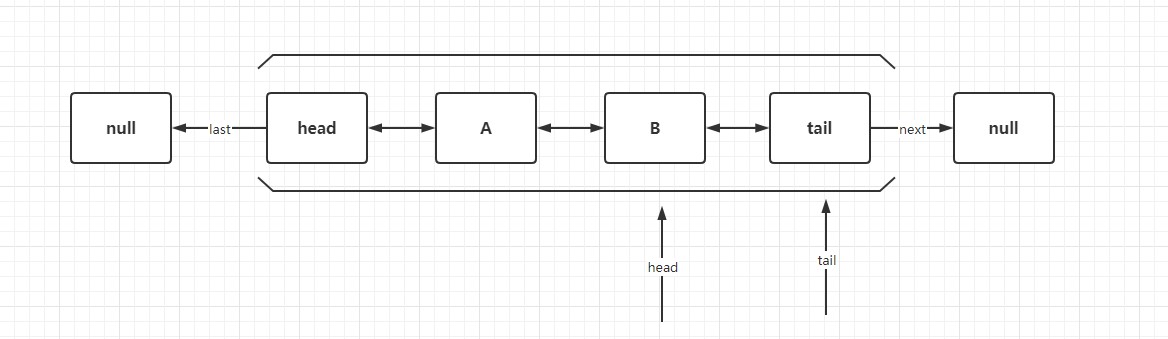
3.2.2 双向链表实现队列

双向链表，取数据从头部获取，添加数据从尾部添加

class LLForQueue {

    DoubleNode head;

    DoubleNode tail;

    public void add(Integer ele) {
        DoubleNode node = new DoubleNode(ele);
        if(head == null) {
            head = node;
            tail = node;
        }else {
            tail.next = node;
            node.last = tail;
            tail = node;
        }
    }

    public Integer poll() {
        if(head == null) {
            return null;
        }
        Integer ans = head.value;
        if(head == tail) {
            head = null;
            tail = null;
        }else {
            head = head.next;
            head.last = null;
        }

        return ans;
    }
}

/**
     * 双向链表实现队列
     * @param args
     */
public static void main(String[] args) {
    LLForQueue queue = new LLForQueue();
    queue.add(1);
    queue.add(2);
    queue.add(3);
    queue.add(4);

    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());

    queue.add(5);
    queue.add(6);


    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
    System.out.println(queue.poll());
}

3.2.3 数组实现栈

数组实现栈比较简单，只需要维护一个索引即可

3.2.4 数组实现队列

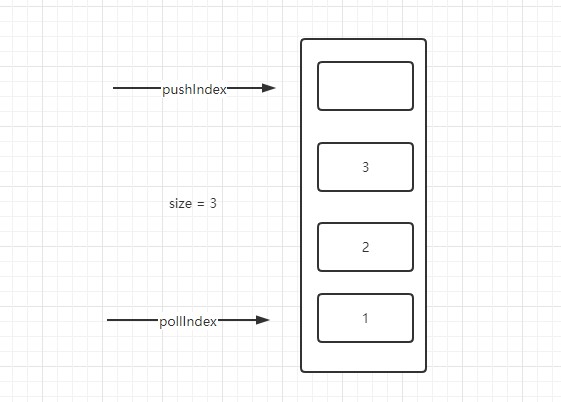
• 定义长度为4的数组
• size用来表示已经存放元素的个数
• pollIndex表示取数的索引位置
• pushIndex表示添加数索引位置

/**
 * 数组实现队列
 */
class ArrayForQueue {

    // 存放数据的数组
    final int[] arr;

    // 获取数据的索引
    int pollIndex = 0;

    // 添加数据的索引
    int pushIndex = 0;

    // 使用数据大小
    int size = 0;

    // 数组长度
    int len;

    ArrayForQueue(int capicity) {
        len = capicity;
        arr = new int[capicity];
    }


    public void add(Integer ele) {
        if(size >= len) throw new RuntimeException("队列已满");
        size++;
        arr[pushIndex] = ele;

        pushIndex = nextIndex(pushIndex);
    }

    private int nextIndex(int index) {
        return (++index) % len;
    }

    public Integer poll() {
        if(size == 0) throw new RuntimeException("队列无数据");

        size--;

        Integer ans = arr[pollIndex];
        pollIndex = nextIndex(pollIndex);

        return ans;
    }
}

3.2.5 栈中获取最小数

实现一个特殊的栈，在基本功能的基础上，再实现返回栈中最小元素的功能

• pop、push、getMin操作的时间复杂度都是 O(1)
• 设计的栈类型可以使用现成的栈结构

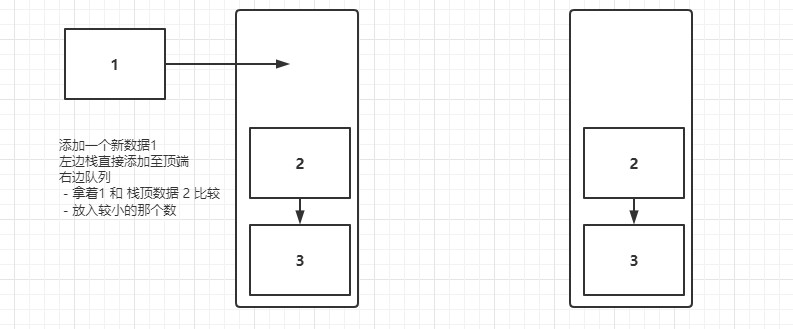
思路：

• 创建一个新的栈，专门用来给用户返回最小值
• 没网数据栈中添加一个数据，都往新栈中添加一个数据
• 至于添加的数是，栈中添加的数和新栈中的栈顶数据进行比较，添加小的那个
• 删除数据时，同时需要删除最小栈中栈顶数据
• 这样就能保证栈中不同高度中的最小值为最小栈中栈顶数据

class LLForStack {

    DoubleNode head;

    public void add(Integer ele) {
        DoubleNode node = new DoubleNode(ele);
        if(head == null) {
            head = node;
        }else {

            node.next = head;
            head.last = node;
            head = node;
        }
    }

    public Integer poll() {
        if(head == null) {
            return null;
        }
        Integer ans = head.value;
        head = head.next;

        if(head != null)
            head.last = null;

        return ans;
    }

    // 获取数据
    public Integer peek() {
        return head == null ? null : head.value;
    }
}


class StackGetMin{

    private LLForStack commonStack = new LLForStack();
    private LLForStack minStack = new LLForStack();

    // 添加数据
    public void add(Integer ele) {
        commonStack.add(ele);

        Integer headVal = minStack.peek();
        // 最小值栈中无数据 直接添加
        if(headVal == null)
            minStack.add(ele);
        else // 最小值栈中有数据 比较添加
            minStack.add(ele < headVal ? ele : headVal);
    }

    // 获取数据
    public Integer poll() {
        Integer ans = commonStack.poll();
        minStack.poll();
        return ans;
    }

    // 获取最小值
    public Integer getMin() {
        return minStack.peek() == null ? null : minStack.peek();
    }

}


// 测试
public static void main(String[] args) {
    StackGetMin stack = new StackGetMin();

    stack.add(3);
    stack.add(2);
    stack.add(4);
    stack.add(3);
    stack.add(1);

    System.out.println("最小值：" + stack.getMin());
    System.out.println("弹出一个数：" + stack.poll());
    System.out.println("最小值：" + stack.getMin());
}

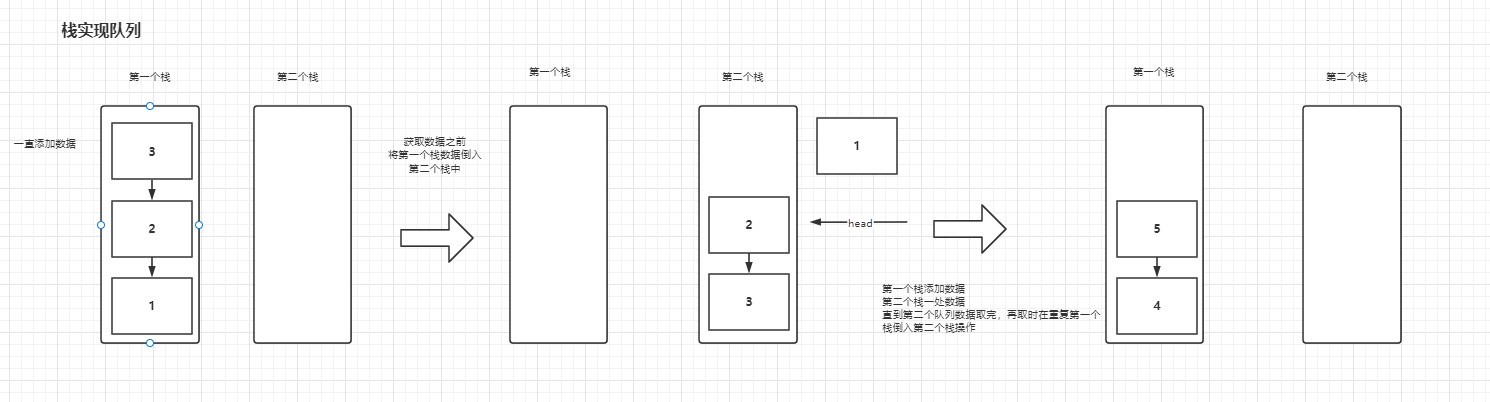
3.2.6 栈实现队列

在只使用栈的情况下实现

思路：

• 将一个栈中的数据倒到另外一个栈中，可以实现队列获取数据顺序
• 一直往一个栈中添加数据
• 当有获取数据的时候，一次性将第一个栈中的数据倒到第二个栈中，注意：需要全部倒完
• 获取数据重第二个栈中获取，直到数据取光，再执型将第一个栈中的数据倒到第二个栈中操作

class LLForStack {

    DoubleNode head;

    public void add(Integer ele) {
        DoubleNode node = new DoubleNode(ele);
        if(head == null) {
            head = node;
        }else {

            node.next = head;
            head.last = node;
            head = node;
        }
    }

    public Integer poll() {
        if(head == null) {
            return null;
        }
        Integer ans = head.value;
        head = head.next;

        if(head != null)
            head.last = null;

        return ans;
    }

    // 获取数据
    public Integer peek() {
        return head == null ? null : head.value;
    }
}


/**
 * 栈实现队列
 */
class StackForQueue {

    LLForStack commonStack = new LLForStack();
    LLForStack getStack = new LLForStack();


    /**
     * 添加数据
     * @param ele
     */
    public void add(Integer ele) {
        commonStack.add(ele);
    }

    /**
     * 获取数据
     * @return
     */
    public Integer poll() {
        // 没有数据
        if(getStack.peek() == null && commonStack.peek() == null)
            return null;

        Integer ans;
        // getStack存在数据
        if((ans = getStack.poll()) != null) {
            return ans;
        }

        // getStack没有数据,将栈1中的数据倒入栈2
        pour();
        // 返回栈2 中的数据
        return getStack.poll();
    }

    // 倒入数据
    private void pour() {
        Integer ele;
        while ((ele = commonStack.poll()) != null) {
            getStack.add(ele);
        }
    }
}

3.2.7 队列实现栈

思路：

和栈实现思想差不多，通过互倒来实现取数顺序

3.3 递归

求数组arr[L..R]中的最大值，怎么用递归方法实现。

1）将[L..R]范围分成左右两半。左：[L..Mid] 右[Mid+1..R] 2）左部分求最大值，右部分求最大值 3） [L..R]范围上的最大值，是max{左部分最大值，右部分最大值}

注意：2）是个递归过程，当范围上只有一个数，就可以不用再递归了

public static void main(String[] args) {
    int[] arr = generateRandomArray(10, 10);
    System.out.println(Arrays.toString(arr));

    // 递归获取最小值
    int min = process(arr, 0, arr.length - 1);
    System.out.println("最小值为：" + min);

}

/**
     * 递归获取最小值
     * @param arr
     * @param left
     * @param right
     * @return
     */
private static int process(int[] arr, int left, int right) {

    if(left == right)
        return arr[left];

    int maxLeft = process(arr, left, left + ((right - left) >> 2));
    int maxRight = process(arr, left + ((right - left) >> 2) + 1, right);

    return Math.min(maxLeft, maxRight);
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

3.4 Master公式

形如 T(N) = a * T(N/b) + O(N^d)(其中的a、b、d都是常数) 的递归函数，可以直接通过Master公式来确定时间复杂度 如果 log(b,a) < d，复杂度为O(N^d) 如果 log(b,a) > d，复杂度为O(N^log(b,a)) 如果 log(b,a) == d，复杂度为O(N^d * logN)

3.5 哈希表和有序表

按值传递

按引用传递

public static void main(String[] args) {
    Integer num1 = new Integer(2);
    Integer num2 = new Integer(2);

    System.out.println(num1 == num2);
    System.out.println(num1.equals(num2));

    HashMap<Integer, Integer> map = new HashMap<>();
    // 基本数据类型的包装类存放到hashmap中会拆包存放，以值传递
    map.put(num1, 1);
    System.out.println(map.containsKey(num2));
}

哈希表

1)哈希表在使用层面上可以理解为一种集合结构 2)如果只有key，没有伴随数据value，可以使用HashSet结构 3)如果既有key，又有伴随数据value，可以使用HashMap结构 4)有无伴随数据，是HashMap和HashSet唯一的区别，实际结构是一回事 5)使用哈希表增(put)、删(remove)、改(put)和查(get)的操作，可以认为时间复杂度为 O(1)，但是常数时间比较大 6)放入哈希表的东西，如果是基础类型，内部按值传递，内存占用是这个东西的大小 7)放入哈希表的东西，如果不是基础类型，内部按引用传递，内存占用是8字节

有序表

1)有序表在使用层面上可以理解为一种集合结构 2)如果只有key，没有伴随数据value，可以使用TreeSet结构 3)如果既有key，又有伴随数据value，可以使用TreeMap结构 4)有无伴随数据，是TreeSet和TreeMap唯一的区别，底层的实际结构是一回事 5)有序表把key按照顺序组织起来，而哈希表完全不组织

6)红黑树、AVL树、size-balance-tree和跳表等都属于有序表结构，只是底层具体实现不同 7)放入如果是基础类型，内部按值传递，内存占用就是这个东西的大小 8)放入如果不是基础类型，内部按引用传递，内存占用是8字节 9)不管是什么底层具体实现，只要是有序表，都有以下固定的基本功能和固定的时间复杂度

第4节：归并排序及其相关面试题

1）整体是递归，左边排好序+右边排好序+merge让整体有序 2）让其整体有序的过程里用了排外序方法 3）利用master公式来求解时间复杂度 4）当然可以用非递归实现

归并排序复杂度

T(N) = 2*T(N/2) + O(N^1)

根据master可知时间复杂度为O(N*logN)

merge过程需要辅助数组，所以额外空间复杂度为O(N)

归并排序的实质是把比较行为变成了有序信息并传递，比O(N^2)的排序快

4.1 递归实现归并排序

/**
     * 通过递归实现归并排序
     */
public static void main(String[] args) {

    // 测试次数
    int testTimes = 1;
    for (int i = 0; i < testTimes; i++) {
        // 生成数组 选择排序使用
        int[] arrSelect = generateRandomArray(10,10);
        // 拷贝数组 归并排序使用
        int[] arrMerge = new int[arrSelect.length];
        System.arraycopy(arrSelect, 0,arrMerge, 0,arrSelect.length);
        System.out.println("初始数组：" + Arrays.toString(arrSelect));

        selectSort(arrSelect);
        System.out.println("选择排序数组：" + Arrays.toString(arrSelect));

        process(arrMerge,0, arrMerge.length - 1);
        System.out.println("归并排序数组：" + Arrays.toString(arrMerge));

        // 对数器比较
        compareRes(arrMerge, arrSelect);
    }


}

/**
     * 结果比较
     * @param arrMerge
     * @param arrSelect
     */
private static void compareRes(int[] arrMerge, int[] arrSelect) {
    for (int i = 0; i < arrMerge.length; i++) {
        if(arrMerge[i] != arrSelect[i]) {
            System.err.println("出错啦");
            break;
        }
    }
}

/**
     * 处理程序
     * @param arr
     * @param left
     * @param right
     */
private static void process(int[] arr, int left, int right) {
    // 剩余一个数
    if(left == right)
        return ;

    int mid = left + ((right - left) >> 1);
    process(arr ,left, mid);
    process(arr ,mid + 1, right);

    // 归并
    merge(arr, left,mid, right);

}

/**
     * 归并
     * @param arr
     * @param left
     * @param right
     */
private static void merge(int[] arr, int left, int mid, int right) {
    int[] help = new int[right - left + 1];
    int helpIndex = 0;
    int leftIndex = left;
    int rightIndex = mid + 1;
    while (leftIndex <= mid && rightIndex <=right) {
        if(arr[leftIndex] > arr[rightIndex]) {
            help[helpIndex++] = arr[rightIndex++];
        }else{
            help[helpIndex++] = arr[leftIndex++];

        }
    }

    while (leftIndex <= mid) {
        help[helpIndex++] = arr[leftIndex++];
    }

    while (rightIndex <= right) {
        help[helpIndex++] = arr[rightIndex++];
    }

    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}


/**
     * 选择排序
     * @param arr
     */
private static void selectSort(int[] arr) {
    if(arr == null || arr.length < 2) return;

    for (int i = 0; i < arr.length - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            // 这里也可以不用记录需要交换的索引，直接交换值(考虑到可能平凡交换这里就记录后面最大值的索引)
            if(arr[minIndex] > arr[j]) minIndex = j;
        }
        // 不相等，说明存在更小的值
        if(i != minIndex) swap(arr, i, minIndex);
    }
}

/**
     * 交换
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

4.2 非递归实现归并排序

思路：

步长为 2*N (N值为1,2,3,4.......)

/**
     * 不用递归
     * 使用步长来实现归并排序
     * @param args
     */
public static void main(String[] args) {

    // 生成数组 选择排序使用
    int[] arr = generateRandomArray(10,10);

    System.out.println("初始化数组为：" + Arrays.toString(arr));

    // 归并排序
    mergeProcess(arr);

    System.out.println("归并排序后数组为：" + Arrays.toString(arr));

}

/**
     *
     * @param arr
     */
private static void mergeProcess(int[] arr) {

    // 步长为 1
    int step = 1;
    int N = arr.length;

    while (step < N) {
        int L = 0;

        while (L < N) {

            int M = L + step - 1;

            if(M >= N)
                break;

            int R = Math.min(N - 1, M + step);

            // 归并
            merge(arr, L,M, R);

            L = R + 1;
        }

        // 步长 * 2
        step <<= 1;

    }
}

/**
     * 归并
     * @param arr
     * @param left
     * @param right
     */
private static void merge(int[] arr, int left, int mid, int right) {
    int[] help = new int[right - left + 1];
    int helpIndex = 0;
    int leftIndex = left;
    int rightIndex = mid + 1;
    while (leftIndex <= mid && rightIndex <=right) {
        if(arr[leftIndex] > arr[rightIndex]) {
            help[helpIndex++] = arr[rightIndex++];
        }else{
            help[helpIndex++] = arr[leftIndex++];

        }
    }

    while (leftIndex <= mid) {
        help[helpIndex++] = arr[leftIndex++];
    }

    while (rightIndex <= right) {
        help[helpIndex++] = arr[rightIndex++];
    }

    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }
}



/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

4.3 小和问题

在一个数组中，一个数左边比它小的数的总和，叫数的小和，所有数的小和累加起来，叫数组小和。求数组小和。 例子： [1,3,4,2,5] 1左边比1小的数：没有 3左边比3小的数：1 4左边比4小的数：1、3 2左边比2小的数：1 5左边比5小的数：1、3、4、 2 所以数组的小和为1+1+3+1+1+3+4+2=16

/**
     * 小和问题
     *
     * 在一个数组中，一个数左边比它小的数的总和，叫数的小和，所有数的小和累加起来，叫数组小和。求数组小和。
     * 例子： [1,3,4,2,5]
     * 1左边比1小的数：没有
     * 3左边比3小的数：1
     * 4左边比4小的数：1、3
     * 2左边比2小的数：1
     * 5左边比5小的数：1、3、4、 2
     * 所以数组的小和为1+1+3+1+1+3+4+2=16
     */
public static void main(String[] args) {
    int[] arr = {7,6,5,8,4,6};


    int sum = process(arr, 0, arr.length - 1);

    System.out.println(sum);

}

private static int process(int[] arr, int left, int right) {
    if(left == right) return 0;

    int midIndex = left + ((right - left) >> 1);
    int leftVal = process(arr, left, midIndex);
    int rightVal = process(arr,midIndex + 1, right);
    int mergeVal = merge(arr, left, midIndex, right);

    return leftVal + rightVal + mergeVal;

}

/**
     * merge
     * @param arr
     * @param left
     * @param midIndex
     * @param right
     */
private static int merge(int[] arr, int left, int midIndex, int right) {
    int pos1 = left;
    int pos2 = midIndex + 1;
    int[] help = new int[right - left + 1];
    int helpIndex = 0;
    int sum = 0;
    while (pos1 <= midIndex && pos2 <= right) {
        // 左边组小于右组才拷贝左组数
        if(arr[pos1] < arr[pos2]) {
            sum += arr[pos1] * (right - pos2 + 1);
            help[helpIndex++] = arr[pos1 ++];
        }else{
            help[helpIndex++] = arr[pos2++];
        }
    }

    while (pos1 <= midIndex) {
        help[helpIndex++] = arr[pos1++];
    }

    while (pos2 <= right) {
        help[helpIndex++] = arr[pos2++];
    }

    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }

    return sum;
}

4.3 归并排序补充题目（难）

https://leetcode.com/problems/count-of-range-sum/

给定一个数组arr，两个整数lower和upper，

返回arr中有多少个子数组的累加和在[lower,upper]范围上

思路分析：

给出数组arr为 [1,-2,2,-3]，子数组累加和范围为[lower,upper]（比如：[-1,1]）

• 前缀和数组：[1,-1,1,-2]
• 假设子数组为[i, j]
• 计算i 到j 下标数组上的和等价与 0~j数组和 - 减去 0 ~ i数组和
• 这里以X位子元素为例
• 原先[lower,upper] 范围变成 [X - upper, X - lower]
• 相当于找出 0 ~ X 访问和在 [X - upper, X - lower]的个数
• 然后使用归并
• 归并中会会使用窗口的概念，应为每部分数组都输有序的递增的所以窗口也是递增滑动的，这里才是核心，

/**
     * leetcode测试题
     * 给定一个数组arr，两个整数lower和upper，
     * 返回arr中有多少个子数组的累加和在[lower,upper]范围上
     */
public static void main(String[] args) {
    // 目标数组
    int[] arr = {1,-2,2,-3};

    // 生成和数组
    int[] helpArr = sumHelpArr(arr);

    // 上边界 下边界
    int upper = 1, lower = -1;

    int count = process(helpArr,0, arr.length - 1, lower,upper);
    System.out.println("出现数量为：" + count);
    System.out.println(Arrays.toString(arr));
}

/**
     * 和辅助数组
     * @param arr
     */
private static int[] sumHelpArr(int[] arr) {
    int[] helpArr = new int[arr.length];
    helpArr[0] = arr[0];

    for (int i = 1; i < arr.length; i++) {
        helpArr[i] = helpArr[i - 1] + arr[i];
    }

    return helpArr;
}

private static int process(int[] arr,int L, int R ,int lower, int upper) {
    // 相等时代表只有一个元素
    if(L == R) {
        // 只有一个元素，代表当前的是0~到当前数(右边界的累加和)，直接判断
        if(arr[L] >= lower && arr[L] <= upper) {
            // 在范围内返回1个
            return 1;
        }else{
            // 不在范围内返回0个
            return 0;
        }
    }

    // 存在多个元素时
    // 需要递归继续分
    int mid = L + ((R - L) >> 1);

    int leftPart = process(arr, L, mid, lower, upper);
    int rightPart = process(arr, mid + 1, R, lower, upper);

    // 归并过程
    int mergePart = merge(arr, L, mid, R, lower, upper);

    // 结果为上面三个数的和
    return leftPart + rightPart + mergePart;
}

/**
     * 归并逻辑
     * @param arr
     * @param L
     * @param M
     * @param R
     * @param lower
     * @param upper
     * @return
     */
private static int merge(int[] arr, int L, int M, int R, int lower, int upper) {
    int ans = 0;
    int MIndex = M + 1;

    int windowLIndex = L, windowRIndex = L;

    while (MIndex <= R) {
        int min = arr[MIndex] - upper;
        int max = arr[MIndex] - lower;

        while (windowLIndex <= M && arr[windowLIndex] < min) // 窗口左边相等不滑动
            windowLIndex ++;

        while (windowRIndex <= M && arr[windowRIndex] <= max) // 窗口右边边相等滑动
            windowRIndex ++;

        ans += (windowRIndex - windowLIndex);

        MIndex ++;
    }


    int[] help = new int[R - L + 1];
    int helpIndex = 0;
    int leftIndex = L;
    int rightIndex = M + 1;
    while (leftIndex <= M && rightIndex <= R) {
        if(arr[leftIndex] > arr[rightIndex]) {
            help[helpIndex++] = arr[rightIndex++];
        }else{
            help[helpIndex++] = arr[leftIndex++];

        }
    }

    while (leftIndex <= M) {
        help[helpIndex++] = arr[leftIndex++];
    }

    while (rightIndex <= R) {
        help[helpIndex++] = arr[rightIndex++];
    }

    for (int i = 0; i < help.length; i++) {
        arr[L + i] = help[i];
    }

    return ans;
}

4.4 快速排序 - Partition过程

给定一个数组arr，和一个整数num。请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。

要求额外空间复杂度O(1)，时间复杂度O(N)

思路：

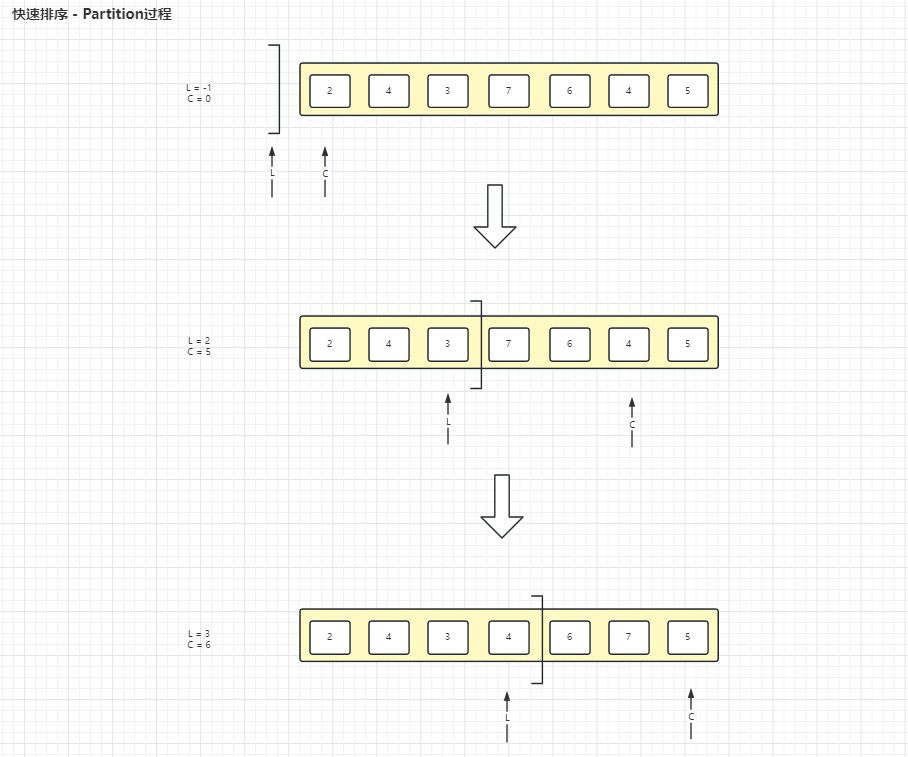
• 举例数组[2, 4, 3, 7, 6, 4, 5 ]，num为 5
• 定义一个左边索引称之为 L，初始化为-1， 只要在L左边(包含L)都是比 5小的
• 同时定义一个当前索引C，初始在0位置
• 当C < 数组长度 LEN时一直出于循环判断状态
• 判断状态时：
  • C索引上的数 < num时，L + 1位置的数和C索引位置上的数相交换，并且 L++，C++，这样可以保证L左边都有序
  • C索引上的数 >= num时，C++即可
  • 这里就好比，L和C中间夹杂着的是>=num的数

public static void main(String[] args) {

    int[] arr = generateRandomArray(5, 10);
    int target = arr[2];

    System.out.println("原始数组：" + Arrays.toString(arr) + "目标数为：" + target);

    partition(arr, target);

    System.out.println("结果数组：" + Arrays.toString(arr));


}

/**
     * 逻辑
     * @param arr
     */
private static void partition(int[] arr, int T) {
    int L = -1;
    int R = arr.length;
    int C = 0;
    while (C < R) {
        if(arr[C] < T) {
            swap(arr, L + 1, C);
            L++;
        }
        C++;
    }
}

/**
     * 索引交换数据
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

4.5 荷兰国旗问题

给定一个数组arr，和一个整数num。请把小于num的数放在数组的左边，等于num的数放在中间，大于num的数放在数组的右边。

要求额外空间复杂度O(1)，时间复杂度O(N)

思路：

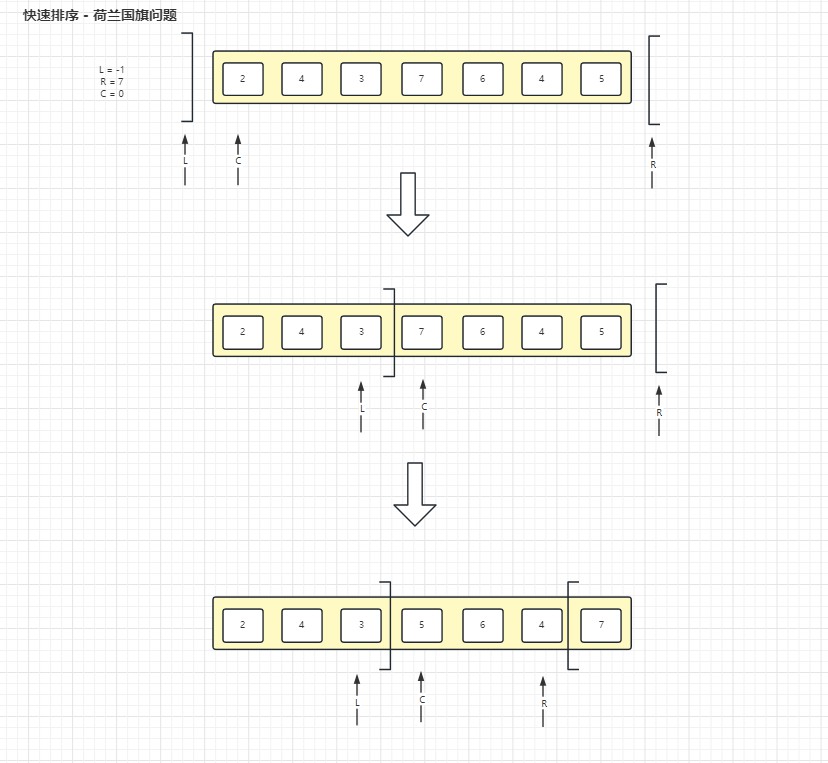
• 思路和上面差不多，只是多了个右范围，并且循环判断时需要注意
• 定义一个左边索引称之为 L，初始化为-1， 只要在L左边(包含L)都是比 5小的
• 定义一个左边索引称之为 R，初始化为数组长度， 只要在R右边(包含R)都是比 5大的
• 判断状态时：
  • C位置数小于num，L + 1位置的数和C索引位置上的数相交换，并且 L++，C++，这样可以保证L左边都有序
  • C位置数等于num，C++
  • C位置数大于num，R -1 位置的数和C索引位置上的数相交换，并且R--，这样可以保证R右边边都有序，需要注意的是C不能++操作，因为交换过来的数还未查看大小

public static void main(String[] args) {

    int[] arr = generateRandomArray(10, 10);
    int target = arr[5];

    System.out.println("原始数组：" + Arrays.toString(arr) + "目标数为：" + target);

    partition(arr, target);

    System.out.println("结果数组：" + Arrays.toString(arr));


}

/**
     * 逻辑
     * @param arr
     */
private static void partition(int[] arr, int T) {
    int L = -1;
    int R = arr.length;
    int C = 0;
    while (C < R) {
        if(arr[C] == T)
            C++;

        if(arr[C] < T) {
            swap(arr, L + 1, C);
            L++;
            C++;

        }

        // 当前数和右边界交换后，当前数不能++,应为交换过来的数没有瞅过
        if(arr[C] > T) {
            swap(arr, R  - 1, C);
            R--;

        }

    }
}

/**
     * 索引交换数据
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

4.6 荷兰国旗问题改版

给定一个数组arr，和一个整数num，这个整为arr数组最后一个位数（arr[arr.length - 1]）。请把小于num的数放在数组的左边，等于num的数放在中间，大于num的数放在数组的右边。

要求额外空间复杂度O(1)，时间复杂度O(N)

思路

• 和荷兰国旗思路一样
• 右侧范围改为arr.length - 1
• 最后结果判断中间数是否存在num，存在就和最右侧的的互换

public static void main(String[] args) {

    int[] arr = {-8, -1, -6, 4, -4, 0, -2, -7, 9, 3};
    int target = arr[arr.length - 1];

    System.out.println("原始数组：" + Arrays.toString(arr) + "目标数为：" + target);

    partition(arr, target);

    System.out.println("结果数组：" + Arrays.toString(arr));


}

/**
     * 逻辑
     * @param arr
     */
private static int[] partition(int[] arr, int T) {
    int L = -1;
    int R = arr.length - 1;
    int C = 0;
    while (C < R) {
        if(arr[C] == T)
            C++;

        else if(arr[C] < T) {
            swap(arr, L + 1, C);
            L++;
            C++;

        }

        // 当前数和右边界交换后，当前数不能++,应为交换过来的数没有瞅过
        else if(arr[C] > T) {
            swap(arr, R  - 1, C);
            R--;

        }
    }
    //        // 判断L 和 R是否紧挨着， 如果是代表中间不存在num数
    //        if((L + 1) == R) {
    //            // L 和 R紧挨着， 不存在中间num数，R和数组最后一个数交换
    //            swap(arr ,R, arr.length - 1);
    //        }else {
    //            // L 和 R不紧挨着， 存在中间num数，R前面一个数和数组最后一个数交换
    //            swap(arr ,R - 1, arr.length - 1);
    //        }

    // 上面的一顿分析可以最终写成 ， R 和 数组最后一个数交换，无需关心L和R中间是否夹着num数，哪怕是存在R和arr.length - 1 的数交换玩后 R位子数>= R-1位置数
    swap(arr ,R, arr.length - 1);

    return new int[]{L + 1, R};
}

/**
     * 索引交换数据
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

4.6 快排

x < mum | x = num(左侧) ......... x = num(右侧) | x > num

在荷兰国旗问题改版中，执行一次就能规定一个数或者一组数(这就是快排1.0和2.0的区别)

mun为每次荷兰国旗问题的范围最右侧的数

比如说，一次荷兰国旗运行后，会出现两个段

• x < mum
• x = num(左侧) ......... x = num(右侧)
• x > num

然后在左侧数组上执行，num就为左侧数组的最后一个数，右侧端也是一样

主要思想就是利用荷兰国旗问题，每次执行就能定下来一个数或者多个数，然后利用递归实现调用

4.6.1 快排 1.0

按照上面描述，每次执行定一个数，x = num(右侧)

4.6.2 快排 2.0

按照上面描述，每次执行定一组数， [x = num(左侧) , x = num(右侧) ]

public static void main(String[] args) {

    int[] arr = generateRandomArray(10, 10);
    int target = arr[arr.length - 1];

    System.out.println("原始数组：" + Arrays.toString(arr) + "目标数为：" + target);

    quickSort2(arr, 0, arr.length - 1);

    System.out.println("结果数组：" + Arrays.toString(arr));


}

/**
     * 快排
     * @param arr
     * @param L
     * @param R
     */
private static void quickSort2(int[] arr, int L, int R) {
    if(L >= R)
        return;
    int[] TRange = partition(arr, L, R);
    System.out.println(Arrays.toString(TRange));
    quickSort2(arr, L, TRange[0] - 1);
    quickSort2(arr, TRange[1] + 1, R);
}

/**
     * 逻辑
     * @param arr
     */
private static int[] partition(int[] arr, int L , int R) {
    int last = R;
    int T = arr[R];
    int C = L;
    L--;
    while (C < R) {
        if(arr[C] == T)
            C++;

        else if(arr[C] < T) {
            swap(arr, L + 1, C);
            L++;
            C++;

        }

        // 当前数和右边界交换后，当前数不能++,应为交换过来的数没有瞅过
        else if(arr[C] > T) {
            swap(arr, R  - 1, C);
            R--;

        }
    }
    //        // 判断L 和 R是否紧挨着， 如果是代表中间不存在num数
    //        if((L + 1) == R) {
    //            // L 和 R紧挨着， 不存在中间num数，R和数组最后一个数交换
    //            swap(arr ,R, arr.length - 1);
    //        }else {
    //            // L 和 R不紧挨着， 存在中间num数，R前面一个数和数组最后一个数交换
    //            swap(arr ,R - 1, arr.length - 1);
    //        }

    // 上面的一顿分析可以最终写成 ， R 和 数组最后一个数交换，无需关心L和R中间是否夹着num数，哪怕是存在R和arr.length - 1 的数交换玩后 R位子数>= R-1位置数
    swap(arr ,R, last);

    return new int[]{L + 1, R};
}

/**
     * 索引交换数据
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

4.6.3 随机快排

在上面题目基础上，数组右侧的值和当前单位内数组任意值交换

public static void main(String[] args) {

    int[] arr = generateRandomArray(10, 10);
    int target = arr[arr.length - 1];

    System.out.println("原始数组：" + Arrays.toString(arr) + "目标数为：" + target);

    quickSort2(arr, 0, arr.length - 1);

    System.out.println("结果数组：" + Arrays.toString(arr));


}

/**
     * 快排
     * @param arr
     * @param L
     * @param R
     */
private static void quickSort2(int[] arr, int L, int R) {
    if(L >= R)
        return;
    // 相对于快排2.0就是多了这一行代码，数组右侧数随机
    swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
    int[] TRange = partition(arr, L, R);
    System.out.println(Arrays.toString(TRange));
    quickSort2(arr, L, TRange[0] - 1);
    quickSort2(arr, TRange[1] + 1, R);
}

/**
     * 逻辑
     * @param arr
     */
private static int[] partition(int[] arr, int L , int R) {
    int last = R;
    int T = arr[R];
    int C = L;
    L--;
    while (C < R) {
        if(arr[C] == T)
            C++;

        else if(arr[C] < T) {
            swap(arr, L + 1, C);
            L++;
            C++;

        }

        // 当前数和右边界交换后，当前数不能++,应为交换过来的数没有瞅过
        else if(arr[C] > T) {
            swap(arr, R  - 1, C);
            R--;

        }
    }
    //        // 判断L 和 R是否紧挨着， 如果是代表中间不存在num数
    //        if((L + 1) == R) {
    //            // L 和 R紧挨着， 不存在中间num数，R和数组最后一个数交换
    //            swap(arr ,R, arr.length - 1);
    //        }else {
    //            // L 和 R不紧挨着， 存在中间num数，R前面一个数和数组最后一个数交换
    //            swap(arr ,R - 1, arr.length - 1);
    //        }

    // 上面的一顿分析可以最终写成 ， R 和 数组最后一个数交换，无需关心L和R中间是否夹着num数，哪怕是存在R和arr.length - 1 的数交换玩后 R位子数>= R-1位置数
    swap(arr ,R, last);

    return new int[]{L + 1, R};
}

/**
     * 索引交换数据
     * @param arr
     * @param i
     * @param j
     */
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}


/**
     * 生成随机数组
     * @param len
     * @param maxVal
     * @return
     */
private static int[] generateRandomArray(int len, int maxVal) {
    int[] arr = new int[len];

    for (int i = 0; i < len; i++) {
        // Math.random()                        [0,1)
        // Math.random() * (maxVal + 1)         [0,maxVal + 1)
        // (int) (Math.random() * (maxVal + 1)) [0,maxVal]
        arr[i] = (int) (Math.random() * (maxVal + 1)) - (int) (Math.random() * (maxVal + 1));
    }
    return arr;
}

第5节：堆和堆排序

5.1 比较器

比较器的实质就是重载比较运算符

比较器可以很好的应用在特殊标准的排序上

比较器可以很好的应用在根据特殊标准排序的结构上

写代码变得异常容易，还用于范型编程

public int compare(T o1, T o2) ;

返回负数的情况，就是o1比o2优先的情况
返回正数的情况，就是o2比o1优先的情况
返回0的情况，就是o1与o2同样优先的情况

案例

public static void main(String[] args) {
    List<Integer> list = Arrays.asList(1, 3, 4, 3, 2, 8, 5, 7);

    list.sort(new CustomComparator());
    System.out.println(list);
}


// 比较器
static class CustomComparator implements Comparator<Integer> {

    // 返回负数： 第一个数前面数在前
    // 返回0： 都可以
    // 返回1：第二个数在前面
    @Override
    public int compare(Integer o1, Integer o2) {
        return o1 > o2 ? -1 : 1;
    }
}

5.2 堆结构

这里所说的堆是一种数据结构，它不同于堆栈区所谓的堆，堆是一种二叉树形式，它存储形式是顺序存储，逻辑上又是二叉树形式。堆有大堆和小堆。大堆就是任何节点它的父节点数据都大于孩子节点。小堆反之。 堆在存储结构上看与数组没有区别，但它在逻辑上是一棵所有节点的数据都大于(大堆)或小于(小堆)孩子节点的特殊二叉树。将一个堆从零建起来需要用到之前提到的一些二叉树的父节点与孩子节点之间的关系，建起一个小堆，每向堆尾插入数据，都需要向上调整一次；若父节点数据大于孩子节点，则需要交换父节点与子节点的数据，若不大于则停止调整，这个过程就是向上调整。

当前节点为i获取父节点公式：(i - 1) / 2

当前节点为i获取子左点公式：2 * i + 1

当前节点为i获取子右点公式：2 * i + 2

5.2.1 堆中插入数据并保持堆结构

逻辑：

首相将数据存放到数组尾部

通过公式获取到当前节点的父节点

将添加元素和父节点比较大小，如果新元素比父节点大就交换位置

重复上面操作，直到新元素小于父节点或者新元素位置为0索引位置停止

/**
 * 堆数据插入，同时保证大根堆结构
 */
public class Demo_02_HeapInsert {

    public static void main(String[] args) {
        // 采用数组存储堆数据
        int[] heap = new int[1024];
        // 堆数据长度
        int heapSize = 0;
        // 定义一个集合循环插入数据
        List<Integer> list = Arrays.asList(2,5,6,3,7,9,4);
        for (Integer element : list) {
            // 将新元素添加到尾部
            heap[heapSize] = element;
            // 元素个数加1
            heapSize++;
            heapInsert(heap, heapSize - 1);

        }
        // 打印堆
        printHeap(heap, heapSize);
    }

    /**
     * 打印堆信息
     * @param heap
     * @param heapSize
     */
    private static void printHeap(int[] heap, int heapSize) {
        for (int i = 0; i < heapSize; i++) {
            System.out.println(heap[i]);
        }
    }

    /**
     * 插入数据
     * 将数据插入尾部
     * 将新插入数据和父节点比较
     *  1. 直到小于父节点
     *  2. 或者到达顶部（0位置）
     * @param heap
     * @param index 新元素索引
     */
    private static void heapInsert(int[] heap, int index) {
        // 当新元素大于父节点一直循环
        while (heap[index] > heap[(index - 1) / 2]) {
            // 新元素和父节点交换
            swap(heap, index, (index - 1) / 2);
            // 新元素索引位置变成父节点位置
            index = (index - 1) / 2;
        }
    }

    /**
     * 交换数据
     * @param heap
     * @param eleIndex
     * @param parIndex
     */
    private static void swap(int[] heap, int eleIndex, int parIndex) {
        int temp = heap[eleIndex];
        heap[eleIndex] = heap[parIndex];
        heap[parIndex] = temp;
    }
}

5.2.2 poll数据并保持堆结构

逻辑：

将头（0）位置数据复制给一个变量，待返回

将尾部数据放到头（0）位置

将头位置数据下沉

根据公司获取需要下沉节点的左孩子节点和右孩子节点

如果需要下沉的节点小于子节点则交换位置，知道需要下沉的节点没有子节点

/**
 * 取出顶部数据，并保持堆结构
 */
public class Demo_03_Heapify {

    public static void main(String[] args) {
        // 采用数组存储堆数据
        int[] heap = new int[1024];
        // 堆数据长度
        int heapSize = 0;
        // 定义一个集合循环插入数据
        List<Integer> list = Arrays.asList(2,5,6,3,7,9,4);
        for (Integer element : list) {
            // 将新元素添加到尾部
            heap[heapSize] = element;
            // 元素个数加1
            heapSize++;
            heapInsert(heap, heapSize - 1);

        }
        // 打印堆
        printHeap(heap, heapSize);
        System.out.println("===================== poll ===================== ");
        // poll
        int num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
        // poll
        num = poll(heap, heapSize);
        System.out.println(num);
        heapSize--;
    }

    /**
     * poll数据
     * @param heap
     * @param heapSize
     * @return
     */
    private static int poll(int[] heap, int heapSize) {
        // 记录顶数据，并返回
        int num = heap[0];
        // 返回数据前需要保持堆结构
        heapify(heap,heapSize);

        return num;
    }

    /**
     * 逻辑就是将堆最后一个数据放到堆顶，让其下沉
     * 当这个数据比两个子元素都大停止，或者没有子元素停止
     * @param heap
     * @param heapSize
     */
    private static void heapify(int[] heap, int heapSize) {
        // 将尾部数据放入头部
        heap[0] = heap[heapSize - 1];
        int eleIndex = 0;
        // 左孩
        int left = eleIndex * 2 + 1;
        // 右孩
        int right = left + 1;
        // 下沉操作
        // 当前元素存在子节点
        while (left < heapSize) {
            // 获取左右孩子节点较大节点的索引
            int largest = (right < heapSize) && heap[right] > heap[left] ? right : left;
            if(heap[eleIndex] >= heap[largest])
                break;
            swap(heap, eleIndex, largest);
            eleIndex = largest;
            // 左孩
            left = eleIndex * 2 + 1;
            // 右孩
            right = left + 1;

        }
    }

    /**
     * 打印堆信息
     * @param heap
     * @param heapSize
     */
    private static void printHeap(int[] heap, int heapSize) {
        for (int i = 0; i < heapSize; i++) {
            System.out.println(heap[i]);
        }
    }

    /**
     * 插入数据
     * 将数据插入尾部
     * 将新插入数据和父节点比较
     *  1. 直到小于父节点
     *  2. 或者到达顶部（0位置）
     * @param heap
     * @param index 新元素索引
     */
    private static void heapInsert(int[] heap, int index) {
        // 当新元素大于父节点一直循环
        while (heap[index] > heap[(index - 1) / 2]) {
            // 新元素和父节点交换
            swap(heap, index, (index - 1) / 2);
            // 新元素索引位置变成父节点位置
            index = (index - 1) / 2;
        }
    }

    /**
     * 交换数据
     * @param heap
     * @param eleIndex
     * @param parIndex
     */
    private static void swap(int[] heap, int eleIndex, int parIndex) {
        int temp = heap[eleIndex];
        heap[eleIndex] = heap[parIndex];
        heap[parIndex] = temp;
    }
}